CHAPTER 4 NOTES
The Development
of a New
Atomic Model

Properties of Light

Electromagnetic radiation: an energy wave that can travel through empty space
Wavelength, λ: the distance between two identical points on adjacent waves
Frequency, ν: The number of waves that pass a given point in a period of time
Speed of light, c = 3.00 E 8 m/s within a vacuum

The Photoelectric Effect

The emission of electrons from a metal when light shines on the metal
Quanta: the minimum amount of energy that can be lost or gained by an atom
Energy, E = hν, h = 6.626 E –34 Joules, J
Photon: a particle of electromagetic radiation having zero rest mass and carrying a quantum of energy

Hydrogen-Atom Line-Emission Spectrum

Ground state: the lowest energy state of an atom
Excited state: An atom that has a higher potential energy than in its ground state
Electricity is run through a low pressure gas and then the beam of light that is produced is sent through a prism
The resulting lines of colored light are a line-emission spectrum
Three series of lines are Lyman, Balmer, and Paschen

Bohr Model of the Atom

Linked the atom’s electrons with photon emissions
The electron can only circle the nucleus in specific orbits
Absorbs energy, moves away from nucleus
Emits energy, moves closer to nucleus

Quantum Model of the Atom

DeBroglie: electrons, like light have a wave-particle duality
Heisenberg’s Uncertainty Principle: it is impossible to determine both the position and the velocity of an electron at the same time
Schroedinger Wave Equation: wave properties of electrons described mathematically
Orbitals: 3-D region of probably finding an electron around a nucleus

Quantum Numbers

Specify the properties of atomic orbitals and the properties of electrons
Principal, n: indicates the main energy level of the electron; 1, 2, 3, …
Angular Momentum, l: indicates the shape of the orbital; 0,1,2,…,n-1
Magnetic, m: indicates orientation in space; - l,…,0,…,+ l
Spin, s: +/-

General Rules

Aufbau principle: an electron occupies the lowest energy orbital that can receive it
Pauli exclusion principle: no two electrons in the same atom can have the same set of four quantum numbers
Hund’s rule: orbitals of equal energy are each occupied by one electron before any orbital is occupied by a second electron, and all electrons in singly occupied orbitals have the same spin

Quantum Number Table

n	l	m	s
1	0	0	+
1	0	0	-
2	0	0	+
2	0	0	-
2	1	-1	+
2	1	0	+
2	1	+1	+
2	1	-1	-
2	1	0	-
2	1	+1	-
3	0	0	+
3	0	0	-
3	1	-1	+
3	1	0	+
3	1	+1	+
3	1	-1	-
3	1	0	-
3	1	+1	-

There are some natural divisions in the table. i.e. between the 1 and 2, and 2 and 3 in the first column. You could also further divide the table by separating between the 0 and 1 in the second column.

n	l	m	s
1	0	0	+
1	0	0	-

2	0	0	+
2	0	0	-

2	1	-1	+
2	1	0	+
2	1	+1	+
2	1	-1	-
2	1	0	-
2	1	+1	-

3	0	0	+
3	0	0	-

3	1	-1	+
3	1	0	+
3	1	+1	+
3	1	-1	-
3	1	0	-
3	1	+1	-

Notice how the chart is now broken into a group of two, another group of two, then a group of six, another group of two and then another group of six.
If you were to look at a periodic table and slide the helium over to be next to the hydrogen and then proceed to read the chart from left to right you will notice that it is also set up to be a group of two, another group of two, then a group of six, another group of two and then another group of six.
What it comes down to is that quantum numbers are actually a mathematical representation of the periodic table.

Electron Configuration Notation

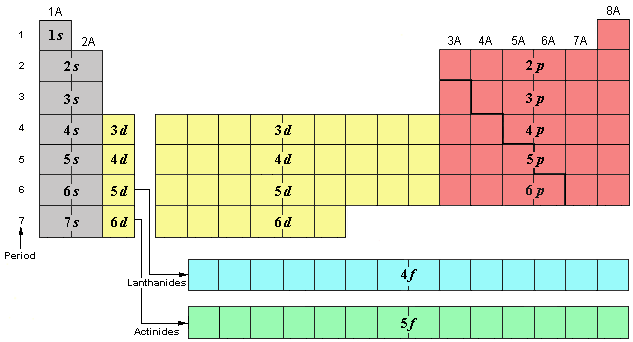The periodic table is broken into regions according to the quantum number table that we had earlier. The n value is called the shell number, the value of l is related to the subshell where 0=s, 1=p, 2=d, and 3=f. A coefficient is then added to show the position of that element within the subshell.

Just writing this information gives the location of that element, or its address. However, to give the full correct electron configuration you need to include all of the completed shells below it.
An example is oxygen which is the fourth member of the 2p subshell so its address is written: 2p⁴. Its overall configuarion would be 1s²2s²2p⁴.
Notice how the coefficients add up to eight and the atomic number of oxygen is eight, so you know you have it set up correctly.

Noble Gas Configuration Notation

Noble Gas Notation is a short cut method of the regular ECN. You go to the Noble gas that occurs before the element that you are looking for and place it in brackets. You then continue with the normal ECN until you get to the element you are looking for. An example of cobalt is shown.
This notation is particularly useful when showing high numbered elements.

Orbital Notation

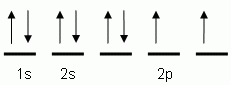
Orbgital notation is similar to ECN except that it breaks everything into its subshells and then represents every electron with its spin. A positive spin is an upward pointing arrow and a negative spin is a downward pointing arrow.
The example shown is for oxygen. Notice that there are eight arrows, and the atomic number for oxygen is eight. Also notice that the 2p orbital has two lone electrons instead of a second pair of electrons. This is becuase it must satisfy Hund's rule which states I have to have one electron in every orbital in a sublevel before a second one can be placed.

Lewis Dot Notation

This is a method of showing how many electrons are available in a particular atom. It can be represented as follows:

	3	6
1	X		4
2	X		7
	5	8

In this diagram the x represents the element symbol and the numbers are where dots would be placed to represent electrons. For example, hydrogen would look like this.


•	H
	H

And oxygen would look like this:

	•	•
•	O		•
•	O
	•

n	l	m	s
1	0	0	+
1	0	0	-
2	0	0	+
2	0	0	-
2	1	-1	+
2	1	0	+
2	1	+1	+
2	1	-1	-
2	1	0	-
2	1	+1	-
3	0	0	+
3	0	0	-
3	1	-1	+
3	1	0	+
3	1	+1	+
3	1	-1	-
3	1	0	-
3	1	+1	-

n	l	m	s
1	0	0	+
1	0	0	-

2	0	0	+
2	0	0	-

2	1	-1	+
2	1	0	+
2	1	+1	+
2	1	-1	-
2	1	0	-
2	1	+1	-

3	0	0	+
3	0	0	-

3	1	-1	+
3	1	0	+
3	1	+1	+
3	1	-1	-
3	1	0	-
3	1	+1	-

n	l	m	s
1	0	0	+
1	0	0	-
2	0	0	+
2	0	0	-
2	1	-1	+
2	1	0	+
2	1	+1	+
2	1	-1	-
2	1	0	-
2	1	+1	-
3	0	0	+
3	0	0	-
3	1	-1	+
3	1	0	+
3	1	+1	+
3	1	-1	-
3	1	0	-
3	1	+1	-

n	l	m	s
1	0	0	+
1	0	0	-

2	0	0	+
2	0	0	-

2	1	-1	+
2	1	0	+
2	1	+1	+
2	1	-1	-
2	1	0	-
2	1	+1	-

3	0	0	+
3	0	0	-

3	1	-1	+
3	1	0	+
3	1	+1	+
3	1	-1	-
3	1	0	-
3	1	+1	-

CHAPTER 4 NOTES The Development of a NewAtomic Model